Current Research Interests
My research interests are in the areas of signal processing, wireless communications, machine learning, and sampling theory.
Below current and past research topics are presented in more detail.
Physical Layer Security
Physical layer security is an approach to implement security directly at the physical layer of a communication system. In the Advanced Communication Systems and Embedded Security Lab (ACES Lab) we experimentally study a modular scheme for semantic security. This form of security is information theoretically provable, and, in contrast to classical key-based encryption, does not rely on the (unproven) assumption that certain mathematical problems are hard to solve. As a consequence, they are inherently secure against quantum computer attacks.
Luis Torres-Figueroa, Ullrich J. Mönich, Johannes Voichtleitner, Anna Frank, Vlad-Costin Andrei, Moritz Wiese, Holger Boche "Experimental Evaluation of a Modular Coding Scheme for Physical Layer Security", 2021 IEEE Global Communications Conference (GLOBECOM), 1-6, 2021 https://doi.org/10.1109/GLOBECOM46510.2021.9685785
Computability in Signal Processing
Turing computability deals with the question of what is theoretically computable on a digital computer. Interestingly, there are non-computable numbers and functions. Since nowadays most signal processing operations are performed on digital computers, the question of computability arises. For example, we analyzed the computability of the Fourier transform and the discrete-time Fourier transform, and showed that there exist well-behaved signals for which the transforms exist mathematically, but cannot be computed on any digital hardware (including CPUs, FPGAs, or DSPs), because the Fourier transforms are not Turing computable. This result also implies that there is no duality between time and frequency domain with respect to computability.
Holger Boche, Ullrich J. Mönich "Computable Time Concentration of Bandlimited Signals and Systems", IEEE Transactions on Signal Processing, vol. 69, pp. 5523-5538, 2021 https://dx.doi.org/10.1109/TSP.2021.3112292
Holger Boche, Ullrich J. Mönich "On the Solvability of the Peak Value Problem for Bandlimited Signals With Applications", IEEE Transactions on Signal Processing, vol. 69, pp. 103-118, 2021. https://dx.doi.org/10.1109/TSP.2020.3042005
Holger Boche, Ullrich J. Mönich "Turing Meets Shannon: Computable Sampling Type Reconstruction With Error Control", IEEE Transactions on Signal Processing, vol. 68, pp. 6350-6365, 2020. https://dx.doi.org/10.1109/TSP.2020.3035913
Holger Boche, Ullrich J. Mönich "Turing Computability of Fourier Transforms of Bandlimited and Discrete Signal", IEEE Transactions on Signal Processing, vol. 68, pp. 532-547, 2020. https://dx.doi.org/10.1109/TSP.2020.2964204
Peak to Average Power Reduction via Tone Reservation
Orthogonal transmission schemes, e.g., orthogonal frequency division multiplexing (OFDM), are widely used in modern communication systems, because of many desirable properties. However, one drawback is the large peak to average power ratio (PAPR) of such systems. In order to reduce the PAPR, different ideas were developed, among them the popular tone reservation method. In this method, the set of available carriers is partitioned into two sets, the first of which is used to carry the information, and the second of which to reduce the PAPR.
Central questions are: What is the best possible reduction of the PAPR? What is the optimal information set that achieves this reduction, and how can it be found? What is the general structure of the optimal information set? So far, no theoretical results have been available. In a series of publications we study the above questions.
Holger Boche, Ullrich J. Mönich "Peak to Average Power Control via Tone Reservation in General Orthonormal Transmission Systems", IEEE Transactions on Signal Processing, vol. 66, no. 13, pp. 3520-3528, July 2018. https://dx.doi.org/10.1109/TSP.2018.2833816
Holger Boche, Ullrich J. Mönich "Solvability of the PAPR Problem for OFDM with Reduced Compensation Set", Proceedings of the 2018 IEEE International Symposium on Information Theory, pp. 2152-2156, June 2018. https://dx.doi.org/10.1109/ISIT.2018.8437447
Holger Boche, Ullrich J. Mönich, Ezra Tampubolon "Complete Characterization of the Solvability of PAPR Reduction for OFDM by Tone Reservation", Proceedings of the 2017 IEEE International Symposium on Information Theory, pp. 2023-2027, June 2017. https://dx.doi.org/10.1109/ISIT.2017.8006884
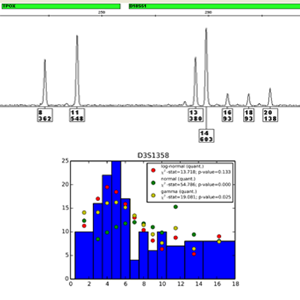
Data Analysis: Forensic DNA Mixtures
Recently a lot of effort has been put in studying fully continuous interpretation approaches for DNA mixtures, where not only the location of a peak is used but also the actual peak heights. Since the peak heights contains additional information, these methods are superior to previous methods, where thresholds have been applied.
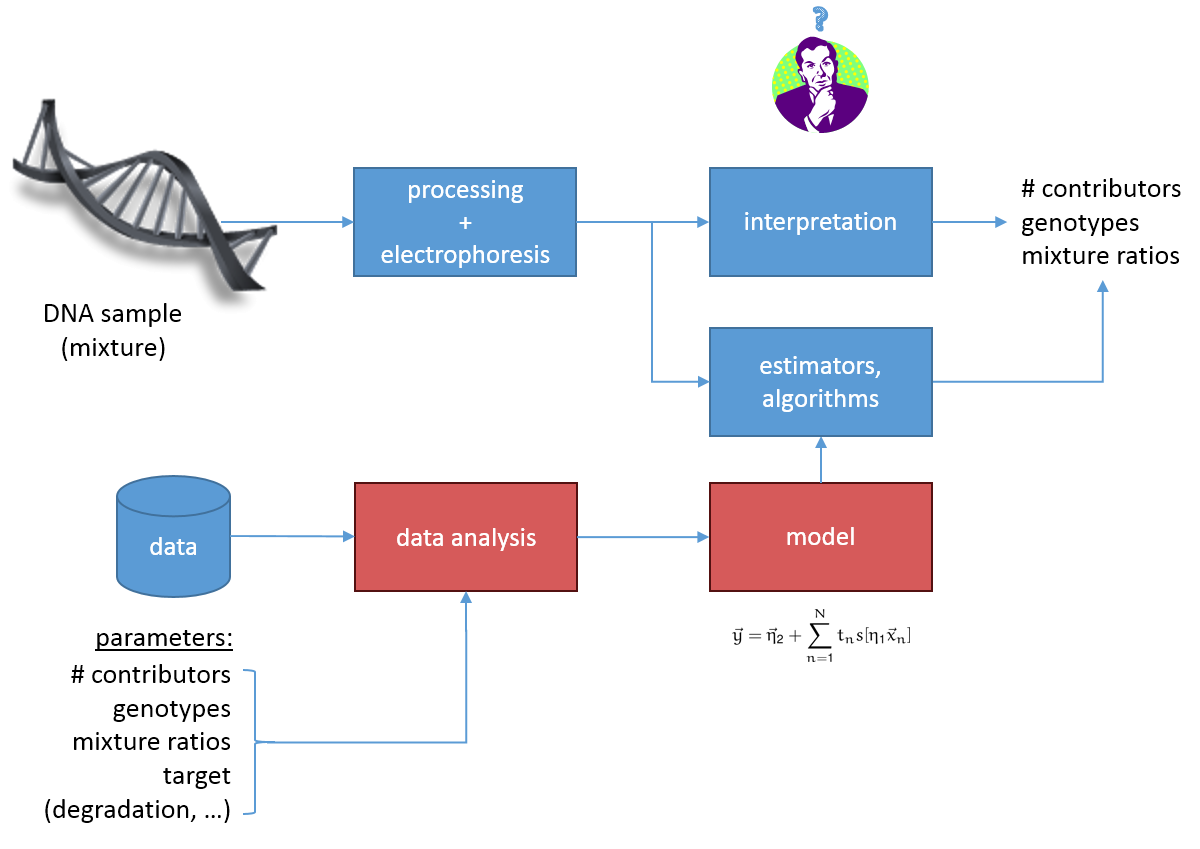
An important step toward the development of these methods is a complete understanding of the statistical properties of the peak heights and the derivation of a signal model. Based on such a model, algorithms for finding the number of contributors in a DNA mixture and for determining the probability that a given suspect contributed to a DNA sample can be developed.
Jakob Valtl, Ullrich J. Mönich, Desmond S. Lun, James Kelley, Catherine M. Grgicak "A series of developmental validation tests for Number of Contributors platforms: Exemplars using NOCIt and a neural network", Forensic Science International: Genetics, vol. 54, 102556, pp. 1-11, 2021 https://doi.org/10.1016/j.fsigen.2021.102556
Ullrich J. Mönich, Ken Duffy, Muriel Médard, Viveck Cadambe, Lauren E. Alfonse, Catherine Grgicak, "Probabilistic Characterisation of Baseline Noise in STR Profiles", Forensic Science International: Genetics, vol. 19, pp. 107-122, November 2015. http://dx.doi.org/10.1016/j.fsigen.2015.07.001
Ullrich J. Mönich, Catherine Grgicak, Viveck Cadambe, Jason Y. Wu, Genevieve. Wellner, Ken Duffy, Muriel Médard, "A signal model for forensic DNA mixtures", in 2014 Asilomar Conference on Signals, Systems and Computers, Nov. 2014. http://www.rle.mit.edu/ncrc/wp-content/uploads/2014/12/asilomar_2014.pdf
Neural Networks
Deep convolutional neural networks have proven their power in numerous applications, e.g., in image and speech processing. However, the theoretical understanding of those networks is difficult and lags behind.
Deformation stability, i.e., the robustness of the network's output to small deformations of the input, is an important property. Recently, for scattering networks, a deformation error stability bound has been established, however, it remained unclear for which signal classes the bound is actually finite.
Johannes Großmann, Michael Koller, Ullrich J. Mönich, Holger Boche, "Shift Invariance and Deformation Error Properties of Deep Convolutional Neural Networks Based on Wavelets" Proceedings of the 2018 IEEE International Workshop on Signal Processing Advances in Wireless Communications (SPAWC), pp. 1-5, June 2018. http://dx.doi.org/10.1109/SPAWC.2018.8446027
Michael Koller, Johannes Großmann, Ullrich J. Mönich, Holger Boche, "Deformation Stability of Deep Convolutional Neural Networks on Sobolev Spaces" Proceedings of the 2018 IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP), pp. 6872-6876, April 2018. http://dx.doi.org/10.1109/ICASSP.2018.8462158
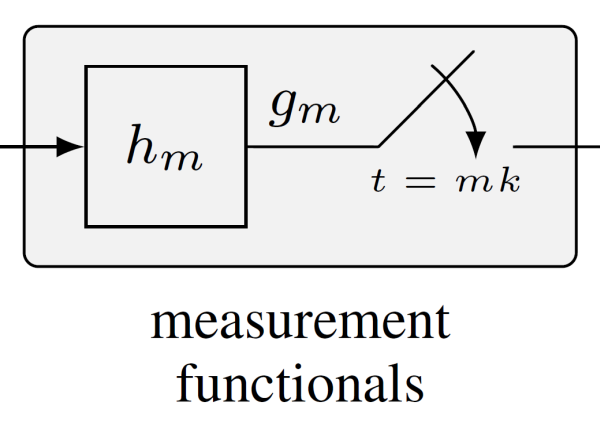
Measurement Functionals / System Approximation
For pointwise sampling it is known that there exist stable LTI systems and functions in the the Paley-Wiener space \(\mathcal{PW}_{\pi}^{1}\) such that the approximation process diverges, regardless of the oversampling factor. Recently, it was shown that the divergence can be overcome by using more general measurement functionals that are based on a complete orthonormal system. However, this approach requires the approximation process to have an increased bandwidth.
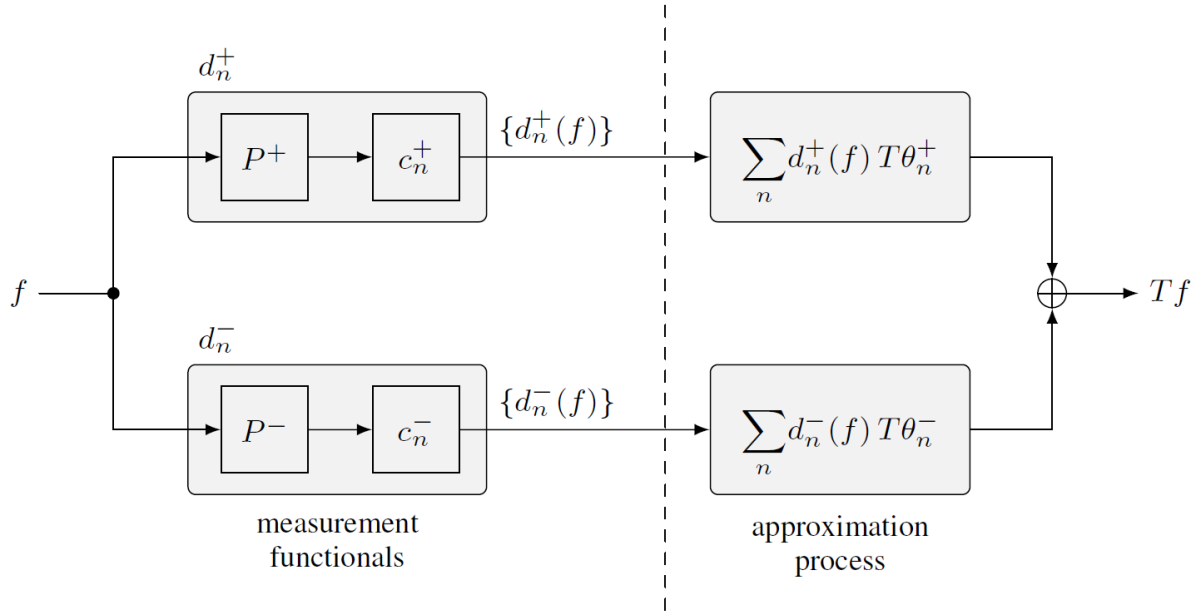
However, there exists a two channel system approximation process that is uniformly convergent for all stable LTI systems and all functions in \(\mathcal{PW}_{\pi}^{1}\). An advantage of the two channel approach compared to the one channel approach is the reduction of the approximation bandwidth, which can be exactly the same as the input function bandwidth.
Ullrich J. Mönich, Holger Boche, "A Two Channel System Approximation for Bandlimited Functions", IEEE Transactions on Information Theory, vol. 63, no. 9, pp. 5496-5505, September 2017. https://dx.doi.org/10.1109/TIT.2017.2724550
Holger Boche, Ullrich J. Mönich, "Signal and System Approximation from General Measurements", in "New Perspectives on Approximation and Sampling Theory - Festschrift in honor of Paul Butzer's 85th birthday", Applied and Numerical Harmonic Analysis, Birkhauser (Springer-Verlag), 2014. http://dspace.mit.edu/handle/1721.1/92323
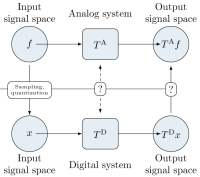
Signal Theory: Signals Reconstruction and System Approximation
Today's information society is based on the power of digital signal processing, and the theoretical foundation for the digital processing of analog signals is the Shannon sampling theorem. Without any further information about the signal, except its bandlimitedness, Nyquist rate sampling is optimal. However, if the signal to exhibits some additional structure, it is possible to reduce the sampling rate below the Nyquist rate. Compressed sensing provides a framework for sampling and recovering of sparse signals, however, sparsity is only one of many possible structures a signal can have.
Since signal processing is concerned with the processing of signals, a fundamental question is: which analog systems can be stably approximated by digital systems? The answer depends on many parameters, like the signal space under consideration, the sampling rate, the kind of sampling, etc. Recently, it has been shown that by using suitable generalized measurement functionals, it is possible to have a uniformly convergent approximation of stable linear time-invariant systems for the space \(\mathcal{PW}_\pi^1\) if oversampling is applied.
Holger Boche, Ullrich J. Mönich, "Signal and System Approximation from General Measurements", arXiv, 2014. http://arxiv.org/abs/1402.1092
Ullrich J. Mönich, Holger Boche, "Non-equidistant sampling for bounded bandlimited signals", Signal Processing, vol. 90, no. 7, pp. 2212-2218, July 2010. http://dx.doi.org/10.1016/j.sigpro.2010.02.002
Previous Research Interests
Quantization in Signal Reconstruction and System Approximation
Quantization and thresholding are two important operations in practical systems. Although quantization is a purely deterministically process, it is usually analyzed stochastically to simplify the mathematical treatment. Quantization and thresholding of signal samples can lead to divergent reconstruction processes. A deterministic treatment of quantization reveals surprising facts. For example, for certain signals the reconstruction error increases unboundedly as the quantization step size is reduced to zero.
Holger Boche, Ullrich J. Mönich, "Behavior of the Quantization Operator for Bandlimited, Nonoversampled Signals", IEEE Transactions on Information Theory, vol. 56, no. 5, pp. 2433-2440, May 2010, http://dx.doi.org/10.1109/TIT.2010.2044072
Component-Based Face Detection
Robust face detection algorithms are important, especially in the computer-human interaction and in surveillance applications. In this work a component-based face detection algorithm is developed, which is more robust in particular in the presence of occlusions. The four face components (eyes, nose, mouth) are detected, using a cascade of boosted classifiers, where the classifiers work with Haar-like features. An online demonstrator is available at http://facedetection.nue.tu-berlin.de/.
Lutz Goldmann, Ullrich J. Mönich, Thomas Sikora, "Components and Their Topology for Robust Face Detection in the Presence of Partial Occlusions", IEEE Transactions on Information Forensics and Security, vol. 2, no. 3, pp. 559-569, Sep. 2007, http://dx.doi.org/10.1109/TIFS.2007.902019
Ullrich J. Mönich, "Objektdetektion basierend auf Komponenten und ihrer Topologie", (Diploma thesis)